Modeling The Capacity-Inventory Relationship

How Variability Affects Inventory

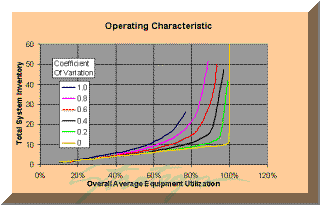
Variability is the reason that inventory rapidly rises with increasing utilization. The amount of variability shapes the curve that defines this relationship. The amount of variability also limits capacity. With high variability, a factory or production line "chokes up" well below theoretical capacity.

The figure below shows how this works. It was developed by simulating a simple production line with perfectly balanced (on average) stations. However, each station's work time may change from cycle to cycle, e.g., variability. The results apply, qualitatively, to most work processes.

The yellow curve shows how inventory varies when all stations are balanced and work times have no variation. At low utilization, workpieces enter the line at well below the maximum production rate and quickly move from station to station. With ten stations and 10% utilization only one workpiece is in the system. It exits before the next is released.

Above 10% (in this case) several workpieces are in the system but each is at a workstation. Above 100% capacity, all stations are full and inventory builds at the line's first station. This is how most production systems are presumed to operate, but they rarely do so because of variability.

With variable work times, shown by the other curves, stations are unsynchronized and inventory collects between them. This inventory buildup begins to accelerate well below 100% utilization. Eventually, the system cannot process work as fast as the inventory builds and output remains constant, even with rising input.

In this particular model, the system choked at about 75% capacity when the coefficient of variation reached 1.0. This explains why many production systems never seem to achieve their potential.

Modeling the System

Simple models often provide deeper insight than complex, "more accurate" models. This paradox is one lesson from the relatively new science of Chaos and from system dynamics. Great teachers from Goldratt to the Buddha used simple examples and parables to convey profound principles.

To study capacity-inventory-variability relationships in production systems, the simple model illustrated above, was constructed using Simul8 software. These are the important features:

• They system is a simple, straight-through production line with 10 sequential stations.

• Each workstation has an average cycle time of 1.0 minute. Hence, the line is perfectly balanced (on average).

• The capacity of this system, based on this average cycle time, is 60 units per hour. This is a production rate corresponding to 100% utilization.

• Workpieces enter the system at regular intervals corresponding to particular production rates from 0% to 100%.

  Workpieces may queue at the head of the line (labeled "Backlog"), if station #1 is not empty.

• Workpieces may queue between stations if the downstream station cannot accept a workpiece when the upstream station releases it.

• The investigator introduces variation by increasing or decreasing the standard deviation of the work times for all stations.

• The independent variable is output rate. The dependent variable is average inventory in the system.

The system was operated with six different values for the work time standard deviation and through a range of workpiece input rates. When inventory stabilized, the results were recorded.