Learning & Experience Curves

Concepts & Continuous Improvement

Learning Curves have traditionally been used for cost estimating and training purposes. However, they have a much wider applications, including Manufacturing and Marketing strategy. They underly the concept of Continuous Improvement. Like compound interest, they generate large benefits from seemingly small, incremental change.

The learning curve came into prominence during World War II when Army Air Force scientists noticed that the cost for a given aircraft model declined with increased production in accordance with a fairly predictable formula. Each time the cumulative production doubled, cost declined by a fixed percentage. In the aircraft industry, at that time, this reduction was about 20%.

The mathematics is a bit complex and is unnecessary for purposes of Manufacturing Strategy. The important thing, for our purposes here, is to understand the general form of the typical curve, how various factors affect the curve and the resulting implications for Manufacturing and Marketing Strategy.

Basic Learning Curve Equation

Learning Curve Equation

Y=Cumulative average cost of X units

K=Cost of unit #1

X=Number of units produced

N=Learning Exponent

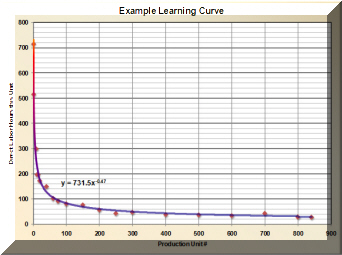
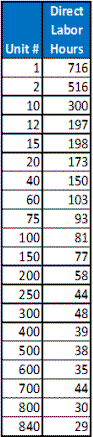
This equation shows the total average cost for all units through the Nth unit. However, the cost of each Nth unit parallels the average cost after 20 or so units. As a practical matter, you can plot the data in Excel and add an exponential trendline.

This linear scale shows direct labor per piece as a function of total pieces produced.

A log-log scale makes the data appear as a straight line. The slope of this line reflects the amount of "learning" that takes place.

Key Features

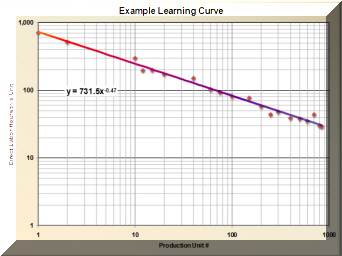
The example above is typical of many situations. Direct labor hours for each unit of production drops rapidly during production startup. The improvement from one unit to the next becomes smaller and smaller but it does continue, often for decades. When plotted on a log-log scale, the data approximates a straight line as shown above right. The slope of this line indicates the intensity of "learning" or improvement. Hence the phrase "steep learning curve" indicates a situation where improvement is coming quickly.

The concept and general form of the function applies to a wide range of industries. It also applies on a wide range of scales from the individual worker performing a specific task to national economies such as China. It works for:

Individuals
Workcells & Work Teams
Factories
Firms
Industries
National Economies

Representative Learning Rates
Aerospace	15%
Shipbuilding	15%-20%
Machine Tools (New Models)	15%-25%
Electronics (Repetitive)	5%-10%
Electrical Wiring (Repetitive)	15%-25%
Machining	5%-10%
Manual Assembly+25% Machining	20%
Manual Assembly+50% Machining	15%
Manual Assembly+75% Machining	10%
Punch Press	5%-10%
Raw Materials	5%-7%
Purchased Parts	12%-15%
Welding (Repetitive)	10%

Most examples in the literature illustrate learning curve effects on direct labor. However, many other dimensions of manufacturing performance follow the same pattern. Examples are quality, delivery and (over the long term) total cost.

The table shows representative learning rates compiled from various sources in the literature. The percentages are the improvement that comes with each doubling of cumulative production. There will be considerable variation from one organization to another within these large categories.

Learning Is Not Pre-Ordained

Performance gains from the learning curve effect are common but not universal. There is no physical law that requires individuals, work groups, companies or industries to learn from their experience. Performance gains come from a variety of mechanisms discussed below but behind these mechanisms is a willingness to learn, an ability to learn and, in many cases, an investment in learning.

Individuals, work groups, companies and industries that do not have the willingness, ability or investment may find their costs declining very little or, even increasing. The most common cause of slow learning is the willingness component that results from corporate or industry arrogance. The Detroit automakers in the 1960's and 1970's possessed a great deal of arrogance that prevented them from learning from the Japanese or even their own experience. It was not until declining market share and bankruptcies forced a bit of humility that these companies began their comeback.

What Determines The Slope

Many factors can determine the learning curve slope for a given individual, team, factory or industry. Among these are:

Management Styles & Actions
Corporate Culture
Organization Structure
Technology
Capital Investment
Engineering

Sources of Cost Improvement

Product Design—As products mature they often go through redesigns. One purpose of this redesign should be making the design easier and less expensive to manufacture. Designers can become more familiar with Design for Manufacturability. Improved coordination and communication between manufacturing and the designers also helps.

Direct Labor Efficiency—improvements in the arrangement of the workplace, improved balancing of work, motivation and improved equipment are among the contributors to direct labor learning.

Indirect Labor Efficiency— material handling, coordination, scheduling, maintenance and other support activities often consume more labor than actual production. Improvements here are just as important as direct labor but are often harder to quantify.

Economies of Scale—large scale equipment may lower costs in several ways. For example one machine with twice the capacity may cost less than two machines with only half the capacity. A small paper machine may require the same size crew as a larger machine but produce far less paper. Sometimes, however, there are dis-economies of scale. Larger factories, for example, often are less efficient than smaller focused factories.

PDF File
.

Plant Layout—An effective plant layout simplifies workflow reduces handling cost and improves coordination. It often reduces inventory as well. Such a layout often implements Cellular Manufacturing and is a first step in Lean Manufacturing initiatives.

Process Improvement—takes many forms at many levels. The small but numerous improvements that result from 5S can be as effective, cumulatively, as a piece of major new equipment. Process improvements can also be simply a change in sequence of operations or the elimination of unnecessary steps.

■ ■ ■ ■ ■ ■ ■

The Strategos Guide To Value Stream and Process Mapping goes beyond symbols and arrows. In over 163 pages it tells the reader how to do it and what to do with it.

Buy Book